Clustering

Justin Donaldson
April-27-2017

Applied Machine Learning 410

(AKA: Birds of a feather)

Clustering History

Clustering first originated in anthropology kroeber

Divide people into culturally similar groups
“…matrilinear descent and avoidance of relatives-in-law were or tended to be inherently connected.”

quant_expression

Clustering Needs

“Data Clustering: 50 Years Beyond K-Means”, A.K. Jain (2008)

Overview

Connectivity Clustering
Centroid-based Clustering
Density-based Clustering
Graph-based Clustering

Connectivity-based clustering

Hierarchical Clustering

Group together observations based on proximity in space.
Agglomerative clustering (clusters grow from individual observations)

Hierarchical Clustering

For this analysis, let's look at arrest rates at a state level.

  head(USArrests)

           Murder Assault UrbanPop Rape
Alabama      13.2     236       58 21.2
Alaska       10.0     263       48 44.5
Arizona       8.1     294       80 31.0
Arkansas      8.8     190       50 19.5
California    9.0     276       91 40.6
Colorado      7.9     204       78 38.7

Hierarchical Clustering

The arrest information is not expressed in distances, so we need to transform it.

  as.matrix(dist(USArrests))[1:6, 1:6]

            Alabama   Alaska   Arizona  Arkansas California Colorado
Alabama     0.00000 37.17701  63.00833  46.92814   55.52477 41.93256
Alaska     37.17701  0.00000  46.59249  77.19741   45.10222 66.47594
Arizona    63.00833 46.59249   0.00000 108.85192   23.19418 90.35115
Arkansas   46.92814 77.19741 108.85192   0.00000   97.58202 36.73486
California 55.52477 45.10222  23.19418  97.58202    0.00000 73.19713
Colorado   41.93256 66.47594  90.35115  36.73486   73.19713  0.00000

Hierarchical Clustering

R provides a good hierarchical clustering method in the standard distribution.

  hc <-hclust(dist(USArrests))
  hc


Call:
hclust(d = dist(USArrests))

Cluster method   : complete 
Distance         : euclidean 
Number of objects: 50

Hierarchical Clustering

Plotting it gives us a representation of the clusters in a tree-like form.

plot(hc, hang=-1)

plot of chunk unnamed-chunk-4

Hierarchical Clustering

We can set a split point using “cutree”, which will give us the desired number of clusters

clusters = cutree(hc, k=5) # cut into 5 clusters
clusters

       Alabama         Alaska        Arizona       Arkansas     California 
             1              1              1              2              1 
      Colorado    Connecticut       Delaware        Florida        Georgia 
             2              3              1              4              2 
        Hawaii          Idaho       Illinois        Indiana           Iowa 
             5              3              1              3              5 
        Kansas       Kentucky      Louisiana          Maine       Maryland 
             3              3              1              5              1 
 Massachusetts       Michigan      Minnesota    Mississippi       Missouri 
             2              1              5              1              2 
       Montana       Nebraska         Nevada  New Hampshire     New Jersey 
             3              3              1              5              2 
    New Mexico       New York North Carolina   North Dakota           Ohio 
             1              1              4              5              3 
      Oklahoma         Oregon   Pennsylvania   Rhode Island South Carolina 
             2              2              3              2              1 
  South Dakota      Tennessee          Texas           Utah        Vermont 
             5              2              2              3              5 
      Virginia     Washington  West Virginia      Wisconsin        Wyoming 
             2              2              5              5              2

Hierarchical Clustering

We can overlay the cluster boundaries on the original plot.

plot(hc)
rect.hclust(hc, k=5, border="purple")

plot of chunk unnamed-chunk-6

Hierarchical Clustering

USArrests[clusters==1,]

               Murder Assault UrbanPop Rape
Alabama          13.2     236       58 21.2
Alaska           10.0     263       48 44.5
Arizona           8.1     294       80 31.0
California        9.0     276       91 40.6
Delaware          5.9     238       72 15.8
Illinois         10.4     249       83 24.0
Louisiana        15.4     249       66 22.2
Maryland         11.3     300       67 27.8
Michigan         12.1     255       74 35.1
Mississippi      16.1     259       44 17.1
Nevada           12.2     252       81 46.0
New Mexico       11.4     285       70 32.1
New York         11.1     254       86 26.1
South Carolina   14.4     279       48 22.5

USArrests[clusters==2,]

              Murder Assault UrbanPop Rape
Arkansas         8.8     190       50 19.5
Colorado         7.9     204       78 38.7
Georgia         17.4     211       60 25.8
Massachusetts    4.4     149       85 16.3
Missouri         9.0     178       70 28.2
New Jersey       7.4     159       89 18.8
Oklahoma         6.6     151       68 20.0
Oregon           4.9     159       67 29.3
Rhode Island     3.4     174       87  8.3
Tennessee       13.2     188       59 26.9
Texas           12.7     201       80 25.5
Virginia         8.5     156       63 20.7
Washington       4.0     145       73 26.2
Wyoming          6.8     161       60 15.6

Hierarchical Clustering

plot of chunk unnamed-chunk-8

Hierarchical Clustering

head(as.matrix(UScitiesD))

           Atlanta Chicago Denver Houston LosAngeles Miami NewYork
Atlanta          0     587   1212     701       1936   604     748
Chicago        587       0    920     940       1745  1188     713
Denver        1212     920      0     879        831  1726    1631
Houston        701     940    879       0       1374   968    1420
LosAngeles    1936    1745    831    1374          0  2339    2451
Miami          604    1188   1726     968       2339     0    1092
           SanFrancisco Seattle Washington.DC
Atlanta            2139    2182           543
Chicago            1858    1737           597
Denver              949    1021          1494
Houston            1645    1891          1220
LosAngeles          347     959          2300
Miami              2594    2734           923

Hierarchical Clustering

hc = hclust(dist(UScitiesD))
plot(hc)
rect.hclust(hc, k=3, border="purple")

plot of chunk unnamed-chunk-10

Hierarchical Clustering

Options - Distance (good defaults)

Euclidean \( \|a-b \|_2 = \sqrt{\sum_i (a_i-b_i)^2} \)
Squared Euclidean \( \|a-b \|_2^2 = \sum_i (a_i-b_i)^2 \)
Manhattan \( \|a-b \|_1 = \sum_i |a_i-b_i| \)
Maximum Distance \( \|a-b \|_\infty = \max_i |a_i-b_i| \)
Mahalanobis Distance : (\( S \) is the covariance matrix)* \( \sqrt{(a-b)^{\top}S^{-1}(a-b)} \)

Hierarchical Clustering

Options - Linkage (good defaults)

single = closest neighbor to any point in cluster gets merged
complete = closest neighbor to furthest point in cluster gets added
UPGMA - Average of distances \( d(x,y) \) : \( {1 \over {|\mathcal{A}|\cdot|\mathcal{B}|}}\sum_{x \in \mathcal{A}}\sum_{ y \in \mathcal{B}} d(x,y) \)
centroid - distance between average of points in cluster.

Centroid-based clustering

K-Means

K-means is the classic centroid-based technique.

  kc <-kmeans(dist(USArrests), 5)
  kc

K-means clustering with 5 clusters of sizes 14, 16, 6, 4, 10

Cluster means:
    Alabama    Alaska   Arizona  Arkansas California  Colorado Connecticut
1  65.89233  96.07457 122.22107  34.09331  107.29421  39.87674    66.23308
2  44.26408  40.63415  39.30706  87.27907   39.61009  72.77326   164.91692
3 186.45199 215.61266 245.68765 140.62960  230.31143 157.96032    64.55080
4 156.66944 185.93502 216.79333 110.42542  202.23294 130.08173    41.33227
5 124.59232 154.48260 183.00204  79.98813  167.54319  95.46898    16.35455
   Delaware   Florida   Georgia    Hawaii     Idaho  Illinois   Indiana
1  67.20616 163.01249  43.25800 128.64955  58.87385  78.34914  62.25396
2  43.22760  67.63373  65.42442 227.97517 155.25746  37.06141 160.84644
3 188.60864 286.62604 162.34794  29.11799  71.09903 201.14674  65.60171
4 159.44839 257.56938 132.83121  48.78623  41.13989 172.61816  38.83723
5 126.21743 224.00494 100.40272  69.53320  17.29587 138.34270  11.73799
       Iowa    Kansas  Kentucky Louisiana     Maine  Maryland
1 119.61759  60.38700  69.05374  77.57022  94.96215 127.67658
2 218.49451 159.05258 165.84901  35.41213 192.58639  40.92104
3  14.16755  67.20859  61.09549 199.77363  36.21497 250.60974
4  27.51177  40.18894  31.37856 170.34344  10.30800 221.15908
5  58.35484  11.41076  16.54525 137.45393  35.62235 188.28510
  Massachusetts  Michigan Minnesota Mississippi  Missouri   Montana
1      33.42978  84.01840 102.76672    91.49070  25.05121  68.73604
2     126.79319  33.19452 202.03634    41.65756  96.36998 165.83229
3     103.59042 207.13296  27.68056   209.69053 130.14358  60.71176
4      77.80478 178.26311  18.60749   179.43873 101.66855  30.98355
5      42.53689 144.48241  41.89394   148.94802  67.55885  15.42239
   Nebraska    Nevada New Hampshire New Jersey New Mexico  New York
1  73.57305  84.13843     118.95531   30.84698  113.01928  83.75387
2 172.20940  39.50211     217.71406  117.34247   34.10491  36.33470
3  54.11084 206.42920      14.53706  114.40486  236.19105 206.64587
4  27.42662 178.22988      26.55704   88.67804  206.94271 178.27364
5  14.93085 143.87782      57.75727   53.05615  173.70919 143.81224
  North Carolina North Dakota      Ohio  Oklahoma    Oregon Pennsylvania
1      166.51660    132.95563  55.24557  28.39951  26.41940     69.14625
2       72.99105    230.82548 153.98042 123.29857 115.23761    168.19979
3      287.09146     18.80491  74.13809 102.55246 111.32739     59.63153
4      256.98193     38.14490  49.16741  74.12040  83.03110     35.61800
5      225.92323     72.29857  15.74348  40.23432  49.30161     13.90017
  Rhode Island South Carolina South Dakota Tennessee     Texas      Utah
1     31.90793      109.20147     92.90532  29.54413  35.75584  56.01761
2    104.36878       38.53295    189.73210  87.15383  74.93990 154.39390
3    127.97252      229.47582     40.03467 139.41307 153.83960  75.56577
4    101.13072      199.39953     10.66362 109.93988 125.76522  52.02789
5     66.64099      168.18393     34.94932  77.62259  91.00713  18.88683
    Vermont  Virginia Washington West Virginia Wisconsin   Wyoming
1 132.66326  26.94074   32.76092      99.77677 121.86942  27.38481
2 229.09553 118.39457  129.17208     195.71986 221.20228 114.20837
3  25.21201 107.17384   98.05935      37.95290  16.55016 111.57683
4  38.98711  78.07427   70.91318      12.67582  32.83759  81.97383
5  73.55590  45.22863   36.11041      42.77453  60.72838  50.17080

Clustering vector:
       Alabama         Alaska        Arizona       Arkansas     California 
             2              2              2              1              2 
      Colorado    Connecticut       Delaware        Florida        Georgia 
             1              5              2              2              1 
        Hawaii          Idaho       Illinois        Indiana           Iowa 
             3              5              2              5              3 
        Kansas       Kentucky      Louisiana          Maine       Maryland 
             5              5              2              4              2 
 Massachusetts       Michigan      Minnesota    Mississippi       Missouri 
             1              2              4              2              1 
       Montana       Nebraska         Nevada  New Hampshire     New Jersey 
             5              5              2              3              1 
    New Mexico       New York North Carolina   North Dakota           Ohio 
             2              2              2              3              5 
      Oklahoma         Oregon   Pennsylvania   Rhode Island South Carolina 
             1              1              5              1              2 
  South Dakota      Tennessee          Texas           Utah        Vermont 
             4              1              1              5              3 
      Virginia     Washington  West Virginia      Wisconsin        Wyoming 
             1              1              4              3              1 

Within cluster sum of squares by cluster:
[1] 274120.554 608986.971  16906.656   5505.797  22532.254
 (between_SS / total_SS =  90.4 %)

Available components:

[1] "cluster"      "centers"      "totss"        "withinss"    
[5] "tot.withinss" "betweenss"    "size"         "iter"        
[9] "ifault"

K-Means

K-means is the classic centroid-based technique.

Assignment Step : \( S_i^{(t)} = \big \{ x_p : \big \| x_p - m^{(t)}_i \big \|^2 \le \big \| x_p - m^{(t)}_j \big \|^2 \ \forall j, 1 \le j \le k \big\} \)
- Assign each data point to cluster whose mean is the smallest within-cluster sum of squares.
Update Step : \( m^{(t+1)}_i = \frac{1}{|S^{(t)}_i|} \sum_{x_j \in S^{(t)}_i} x_j \)
- Calculate new centroids

K-Means

  colors =brewer.pal(5, "Spectral")
  arrests$clusters = colors[kc$cluster]
  ggpairs(arrests, mapping=ggplot2::aes(fill=clusters,color=clusters))

plot of chunk unnamed-chunk-12

K-Means

K-means is more sensitive to scaling

  arrests = data.frame(scale(USArrests))

Quick aside on scaling

Field measurements can have different scales

dat = cbind(
  x=rnorm(100, mean =  0, sd = 1),
  y=rnorm(100, mean = -4, sd = 2),
  z=rnorm(100, mean =  4, sd = 9)
  )

boxplot(dat)

plot of chunk unnamed-chunk-16

Quick aside on scaling

In some cases it may be useful to normalize the scales. Standard normalization:

mean = 0
standard deviation = 1

boxplot(scale(dat))

plot of chunk unnamed-chunk-17

K-means compared to Hierarchical Clustering

Hierarchical Clustering

cluster count can be determined post hoc
linkages are robust against scaling differences in fields
good at extracting “strand” clusters
quadratic time complexity : ~ \( O(n^2) \)
repeatable

K-Means

“k” cluster count must be given up front.
scaling affects centroid calculation, consider normalizing if possible.
good at extracting “spherical” clusters
near-linear time complexity : ~ \( O(n) \)
requires random initialization, results may not be repeatable in some cases

Distribution-based clustering

Bio break? - 15m

Expectation Maximaztion

Expectation Maximization

require(EMCluster)

based on probability distributions
no hard assignment of points to clusters, instead use probabilities
underlying distributions can be anything, gaussians are common

Expectation Maximization

require(EMCluster)

Calculate expected value of log likelihood function: \[ Q(\boldsymbol\theta|\boldsymbol\theta^{(t)}) = \operatorname{E}_{\mathbf{Z}|\mathbf{X},\boldsymbol\theta^{(t)}}\left[ \log L (\boldsymbol\theta;\mathbf{X},\mathbf{Z}) \right] \]
- with respect to the conditional distribution of \( Z \) given \( X \) under the current estimate of the parameters \( \theta^{(t)} \).
Find the parameter that maximizes : \[ \boldsymbol\theta^{(t+1)} = \underset{\boldsymbol\theta}{\operatorname{arg\,max}} \ Q(\boldsymbol\theta|\boldsymbol\theta^{(t)}) \]

Expectation Maximization

Plain english:

Initialize \( \theta \) to one or more random values.
Compute the best value for \( Z \) given the \( \theta \) values.
Then use the computed values to compute a better value for \( \theta \).
Rinse and repeat.

Expectation Maximization

EM works well when you have a good idea of the underlying distribution of the data. In this case, normal deviates

means = c(0,20,-15)
x = rnorm(300, means[1], 10)
y = rnorm(100, means[2], 1)
z = rnorm(100, means[3], 1)
dat = data.frame(x=c(x,y,z))
ggplot(data = dat,aes(x=x)) + geom_histogram()

Expectation Maximization

EM works well when you have a good idea of the underlying distribution of the data. In this case, normal deviates plot of chunk unnamed-chunk-21

Expectation Maximization

library(EMCluster)
sem = shortemcluster(dat, simple.init(dat, nclass = 3))
em = emcluster(dat, sem, assign.class=T)
colors = brewer.pal(3, "Spectral")[em$class]
dat$class = colors
ggplot(data = dat, aes(x=x, fill=class)) + geom_histogram(position="dodge")

plot of chunk unnamed-chunk-22

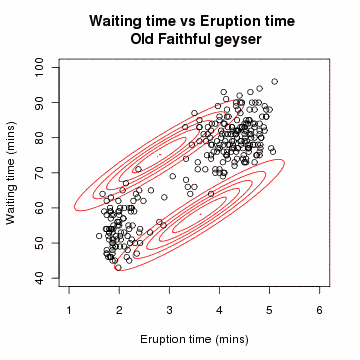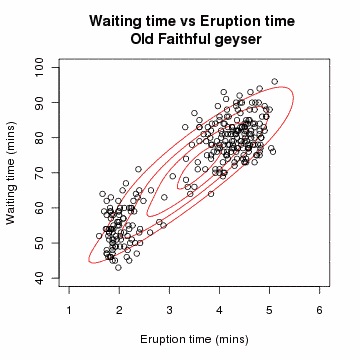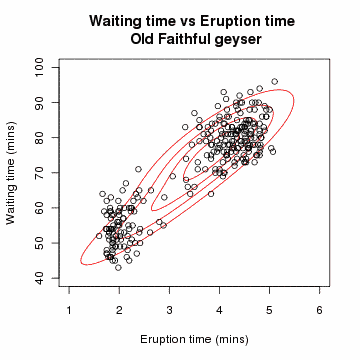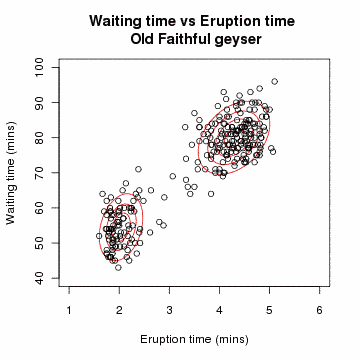
Expectation Maximization

EM models the distribution parameters, and can capture them even if distributions overlap.

em$Mu

            [,1]
[1,]  20.0276881
[2,]   0.4845825
[3,] -15.0464675

as.matrix(means)

     [,1]
[1,]    0
[2,]   20
[3,]  -15

Expectation Maximization

Considerations

If distribution characteristics are known, EM works well at recovering from noise and overlap in cluster boundaries.
Parameterization includes cluster count and mixture model specification.
Most similar to K-means, except cluster assignment is soft, rather than hard as in km.

Expectation Maximization

Strengths:

Can easily adapt to different models/kernels (besides gaussian).
Retrieves clusters and cluster model coefficients!
Fast, iterative algorithm. Complexity depends on number of iterations and time to compute E and M steps.

Weaknesses:

Requires more parameterization up front than any other model(cluster count, model expectation (e.g. gaussian), convergence, tolerance, etc.)
Complexity dependent on chosen model parameters.

Density-based Clustering

DBScan

DBScan

Density-based Spatial Clustering of Applications With Noise Points are:

Core - within \( \epsilon \) of \( p \) (min points).
Reachable - within \( \epsilon \) of a core point.
Outliner - neither are true.

DBScan

Look at iris again

library("dbscan")
data(iris)
iris <- as.matrix(iris[,1:4])
res <- dbscan(iris, eps = .5, minPts = 5)
res

DBSCAN clustering for 150 objects.
Parameters: eps = 0.5, minPts = 5
The clustering contains 2 cluster(s) and 17 noise points.

 0  1  2 
17 49 84 

Available fields: cluster, eps, minPts

DBScan

Look at iris again

library("dbscan")
kNNdistplot(USArrests, k = 5)
eps = 20
abline(h=eps, col = "red", lty=2)

plot of chunk unnamed-chunk-25

res <- dbscan(USArrests, eps = eps, minPts = 3)
res

DBSCAN clustering for 50 objects.
Parameters: eps = 20, minPts = 3
The clustering contains 5 cluster(s) and 10 noise points.

 0  1  2  3  4  5 
10  7  3 10  9 11 

Available fields: cluster, eps, minPts

DBScan

arrests = USArrests
arrests$cluster = factor(res$cluster)
arrests[arrests$cluster ==1,]

          Murder Assault UrbanPop Rape cluster
Alabama     13.2     236       58 21.2       1
Delaware     5.9     238       72 15.8       1
Illinois    10.4     249       83 24.0       1
Louisiana   15.4     249       66 22.2       1
Michigan    12.1     255       74 35.1       1
Nevada      12.2     252       81 46.0       1
New York    11.1     254       86 26.1       1

arrests[arrests$cluster ==2,]

           Murder Assault UrbanPop Rape cluster
Arizona       8.1     294       80 31.0       2
Maryland     11.3     300       67 27.8       2
New Mexico   11.4     285       70 32.1       2

arrests[arrests$cluster ==3,]

             Murder Assault UrbanPop Rape cluster
Connecticut     3.3     110       77 11.1       3
Idaho           2.6     120       54 14.2       3
Indiana         7.2     113       65 21.0       3
Kansas          6.0     115       66 18.0       3
Kentucky        9.7     109       52 16.3       3
Montana         6.0     109       53 16.4       3
Nebraska        4.3     102       62 16.5       3
Ohio            7.3     120       75 21.4       3
Pennsylvania    6.3     106       72 14.9       3
Utah            3.2     120       80 22.9       3

DBScan

arrests = USArrests
arrests$cluster = factor(res$cluster)
ggpairs(arrests, mapping=ggplot2::aes(fill=cluster,color=cluster))

plot of chunk unnamed-chunk-27

DBScan

Scale fields with differing mean/variance in order to prevent one dimension from dominating the NN cluster metric

res <- dbscan(scale(USArrests), eps = 1, minPts = 3)
res

DBSCAN clustering for 50 objects.
Parameters: eps = 1, minPts = 3
The clustering contains 4 cluster(s) and 9 noise points.

 0  1  2  3  4 
 9  6 29  3  3 

Available fields: cluster, eps, minPts

DBScan

arrests = USArrests
arrests$cluster = factor(res$cluster)
ggpairs(arrests, mapping=ggplot2::aes(fill=cluster,color=cluster))

plot of chunk unnamed-chunk-29

DBScan

Strengths:

Does not require cluster count parameter
Finds arbitrary shapes with consistent density
- Avoid “thin line” effect of hierarchical clustering
Excludes outliers from clusters (i.e. can eliminate noise)
Requires two parameters
(Mostly) invariant to ordering

Weaknesses:

Non-deterministic clusters possible during “ties” among neighbors
Suffers from curse of dimensionality issues
Doesn't handle clusters of differing density
Relies on expert knowledge to set \( \epsilon \) and \( p \).
Expensive algorithm \( O(n^2) \), although pre-indexing can yield \( O(log(n)) \).

DBScan

Graph-based Clustering

HCS

Highly Connected Subgraph

Find the minimum cut on a graph
Partition graph into two subgraphs
Recursively run on the subgraphs

HCS

# source("https://bioconductor.org/biocLite.R")
# biocLite("RBGL")
# biocLite("Rgraphviz")
library(RBGL)
library(Rgraphviz)
con <- file(system.file("XML/conn.gxl",package="RBGL"), open="r")
coex <- fromGXL(con)
coex

A graphNEL graph with undirected edges
Number of Nodes = 8 
Number of Edges = 14

HCS

plot(coex)

plot of chunk unnamed-chunk-31

HCS

plot(coex)

plot of chunk unnamed-chunk-32

highlyConnSG(coex)

$clusters
$clusters[[1]]
[1] "A" "B" "C" "D"

$clusters[[2]]
[1] "E" "H" "F" "G"

MCL

MCL - Markov Cluster Algorithm

Process has four phases:
- (Optional-required for directed graphs) add self links
- “Expansion” through standard matrix multiplication
- “Inflation” through column wise exponentiation (I) and renormalization
- Rinse and repeat

Picture courtesy of http://micans.org and Stijn van Dongen

MCL

MCL works with adjacency matrices

library(MCL)
adjacency <- matrix(c(0,1,1,1,0,0,0,0,0,1,0,1,1,1,0,0,0,0,1,1,
                      0,1,0,0,0,0,0,1,1,1,0,0,0,0,0,0,0,1,0,0,
                      0,1,1,0,0,0,0,0,0,1,0,1,0,0,0,0,0,0,1,1,
                      0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0),
                    byrow=TRUE, nrow=9)
library(igraph)
gu<-graph.adjacency(adjacency, mode="undirected")
plot(gu)

plot of chunk unnamed-chunk-34

MCL

Here we're running mcl and adding optional self-loops, and returning an equlibrium state matrix.

res = mcl(x = adjacency, addLoops=TRUE, ESM = TRUE)
res

$K
[1] 3

$n.iterations
[1] 14

$Cluster
[1] 1 1 1 1 2 2 2 0 0

$Equilibrium.state.matrix
  1 2 3 4 5 6 7 8 9
1 0 0 0 0 0 0 0 0 0
2 1 1 1 1 0 0 0 0 0
3 0 0 0 0 0 0 0 0 0
4 0 0 0 0 0 0 0 0 0
5 0 0 0 0 1 1 1 0 0
6 0 0 0 0 0 0 0 0 0
7 0 0 0 0 0 0 0 0 0
8 0 0 0 0 0 0 0 1 0
9 0 0 0 0 0 0 0 0 1

MCL

We can use igraph to plot the network with our clusters

plot(graph.adjacency(adjacency), vertex.color = res$Cluster)

plot of chunk unnamed-chunk-36

Clustering Technique Recap

In general, learn as much as possible about the data before trying to cluster.
- Do you know the expected number of clusters?
- Do you know anything about the distribution?
- Do you know if the data is graph-like?
Simplify structure when/where appropriate (sparsification, network pruningu
Consider combining clustering with dimensionality reduction (coming soon!)

Clustering Deep Dive

imdb top 5000 movies imdb 5000

imdb

dat = read.csv("movie_metadata.csv")
str(dat)

'data.frame':   5043 obs. of  28 variables:
 $ color                    : chr  "Color" "Color" "Color" "Color" ...
 $ director_name            : chr  "James Cameron" "Gore Verbinski" "Sam Mendes" "Christopher Nolan" ...
 $ num_critic_for_reviews   : int  723 302 602 813 NA 462 392 324 635 375 ...
 $ duration                 : int  178 169 148 164 NA 132 156 100 141 153 ...
 $ director_facebook_likes  : int  0 563 0 22000 131 475 0 15 0 282 ...
 $ actor_3_facebook_likes   : int  855 1000 161 23000 NA 530 4000 284 19000 10000 ...
 $ actor_2_name             : chr  "Joel David Moore" "Orlando Bloom" "Rory Kinnear" "Christian Bale" ...
 $ actor_1_facebook_likes   : int  1000 40000 11000 27000 131 640 24000 799 26000 25000 ...
 $ gross                    : int  760505847 309404152 200074175 448130642 NA 73058679 336530303 200807262 458991599 301956980 ...
 $ genres                   : chr  "Action|Adventure|Fantasy|Sci-Fi" "Action|Adventure|Fantasy" "Action|Adventure|Thriller" "Action|Thriller" ...
 $ actor_1_name             : chr  "CCH Pounder" "Johnny Depp" "Christoph Waltz" "Tom Hardy" ...
 $ movie_title              : chr  "Avatar " "Pirates of the Caribbean: At World's End " "Spectre " "The Dark Knight Rises " ...
 $ num_voted_users          : int  886204 471220 275868 1144337 8 212204 383056 294810 462669 321795 ...
 $ cast_total_facebook_likes: int  4834 48350 11700 106759 143 1873 46055 2036 92000 58753 ...
 $ actor_3_name             : chr  "Wes Studi" "Jack Davenport" "Stephanie Sigman" "Joseph Gordon-Levitt" ...
 $ facenumber_in_poster     : int  0 0 1 0 0 1 0 1 4 3 ...
 $ plot_keywords            : chr  "avatar|future|marine|native|paraplegic" "goddess|marriage ceremony|marriage proposal|pirate|singapore" "bomb|espionage|sequel|spy|terrorist" "deception|imprisonment|lawlessness|police officer|terrorist plot" ...
 $ movie_imdb_link          : chr  "http://www.imdb.com/title/tt0499549/?ref_=fn_tt_tt_1" "http://www.imdb.com/title/tt0449088/?ref_=fn_tt_tt_1" "http://www.imdb.com/title/tt2379713/?ref_=fn_tt_tt_1" "http://www.imdb.com/title/tt1345836/?ref_=fn_tt_tt_1" ...
 $ num_user_for_reviews     : int  3054 1238 994 2701 NA 738 1902 387 1117 973 ...
 $ language                 : chr  "English" "English" "English" "English" ...
 $ country                  : chr  "USA" "USA" "UK" "USA" ...
 $ content_rating           : chr  "PG-13" "PG-13" "PG-13" "PG-13" ...
 $ budget                   : num  2.37e+08 3.00e+08 2.45e+08 2.50e+08 NA ...
 $ title_year               : int  2009 2007 2015 2012 NA 2012 2007 2010 2015 2009 ...
 $ actor_2_facebook_likes   : int  936 5000 393 23000 12 632 11000 553 21000 11000 ...
 $ imdb_score               : num  7.9 7.1 6.8 8.5 7.1 6.6 6.2 7.8 7.5 7.5 ...
 $ aspect_ratio             : num  1.78 2.35 2.35 2.35 NA 2.35 2.35 1.85 2.35 2.35 ...
 $ movie_facebook_likes     : int  33000 0 85000 164000 0 24000 0 29000 118000 10000 ...

imdb

sapply(dat, is.numeric)

                    color             director_name 
                    FALSE                     FALSE 
   num_critic_for_reviews                  duration 
                     TRUE                      TRUE 
  director_facebook_likes    actor_3_facebook_likes 
                     TRUE                      TRUE 
             actor_2_name    actor_1_facebook_likes 
                    FALSE                      TRUE 
                    gross                    genres 
                     TRUE                     FALSE 
             actor_1_name               movie_title 
                    FALSE                     FALSE 
          num_voted_users cast_total_facebook_likes 
                     TRUE                      TRUE 
             actor_3_name      facenumber_in_poster 
                    FALSE                      TRUE 
            plot_keywords           movie_imdb_link 
                    FALSE                     FALSE 
     num_user_for_reviews                  language 
                     TRUE                     FALSE 
                  country            content_rating 
                    FALSE                     FALSE 
                   budget                title_year 
                     TRUE                      TRUE 
   actor_2_facebook_likes                imdb_score 
                     TRUE                      TRUE 
             aspect_ratio      movie_facebook_likes 
                     TRUE                      TRUE

imdb

dat_nums = dat[,sapply(dat, is.numeric)]
str(dat_nums)

'data.frame':   5043 obs. of  16 variables:
 $ num_critic_for_reviews   : int  723 302 602 813 NA 462 392 324 635 375 ...
 $ duration                 : int  178 169 148 164 NA 132 156 100 141 153 ...
 $ director_facebook_likes  : int  0 563 0 22000 131 475 0 15 0 282 ...
 $ actor_3_facebook_likes   : int  855 1000 161 23000 NA 530 4000 284 19000 10000 ...
 $ actor_1_facebook_likes   : int  1000 40000 11000 27000 131 640 24000 799 26000 25000 ...
 $ gross                    : int  760505847 309404152 200074175 448130642 NA 73058679 336530303 200807262 458991599 301956980 ...
 $ num_voted_users          : int  886204 471220 275868 1144337 8 212204 383056 294810 462669 321795 ...
 $ cast_total_facebook_likes: int  4834 48350 11700 106759 143 1873 46055 2036 92000 58753 ...
 $ facenumber_in_poster     : int  0 0 1 0 0 1 0 1 4 3 ...
 $ num_user_for_reviews     : int  3054 1238 994 2701 NA 738 1902 387 1117 973 ...
 $ budget                   : num  2.37e+08 3.00e+08 2.45e+08 2.50e+08 NA ...
 $ title_year               : int  2009 2007 2015 2012 NA 2012 2007 2010 2015 2009 ...
 $ actor_2_facebook_likes   : int  936 5000 393 23000 12 632 11000 553 21000 11000 ...
 $ imdb_score               : num  7.9 7.1 6.8 8.5 7.1 6.6 6.2 7.8 7.5 7.5 ...
 $ aspect_ratio             : num  1.78 2.35 2.35 2.35 NA 2.35 2.35 1.85 2.35 2.35 ...
 $ movie_facebook_likes     : int  33000 0 85000 164000 0 24000 0 29000 118000 10000 ...

imdb

mdat = melt(dat_nums, id.vars=c("imdb_score"))
ggplot(mdat, aes(fill=factor(as.integer(imdb_score)), x=value)) + 
  geom_histogram() + 
  facet_wrap(~variable, scales="free")

plot of chunk unnamed-chunk-40

imdb

It can help to scale

mdat = melt(dat_nums, id.vars=c("imdb_score"))
ggplot(mdat, aes(fill=factor(as.integer(imdb_score)), x=value)) + 
  geom_histogram() + 
  scale_x_log10() + 
  facet_wrap(~variable, scales="free")

plot of chunk unnamed-chunk-41

imdb

mdat = melt(dat_nums, id.vars=c("imdb_score"))
ggplot(mdat, aes(factor(as.integer(imdb_score)), value)) + 
  geom_boxplot(outlier.shape=NA) + 
  facet_wrap(~variable, scales="free_y")

plot of chunk unnamed-chunk-42

imdb

It can help to scale

mdat = melt(dat_nums, id.vars=c("imdb_score"))
ggplot(mdat, aes(factor(as.integer(imdb_score)), value)) + 
  geom_boxplot(outlier.shape=NA) + 
  scale_y_log10() + 
  facet_wrap(~variable, scales="free_y")

plot of chunk unnamed-chunk-43

imdb

Impute the means

dat_num_imp = sapply(dat_nums, function(x) {x[is.na(x)]<-mean(x,na.rm=T); x})
any(is.na(dat_num_imp))

[1] FALSE

imdb

Using raw data produces very uneven clusters:

kdat = kmeans(dat_num_imp, 3)
dat$cluster = kdat$cluster
ggplot(dat, aes(x=cluster,fill=factor(cluster))) + geom_histogram(stat="count")

plot of chunk unnamed-chunk-45

imdb

Scaling issues in fields (budget) are dominating cluster categories:

t = table(dat$cluster)
t


   1    2    3 
   1 4678  364

small = names(t)[which.min(t)]
dat[dat$cluster == as.integer(small),c("movie_title", "language", "budget", "cluster")]

     movie_title language      budget cluster
2989   The Host    Korean 12215500000       1

median(dat$budget,na.rm=T)

[1] 2e+07

imdb

We can scale the data so it has the same column-wise mean/variance:

dat_scaled = as.data.frame(scale(dat_num_imp))
kdat = kmeans(dat_scaled, 3)
table(kdat$cluster)


   1    2    3 
4164  765  114

ds = dat_scaled
ds$cluster = kdat$cluster
dat$cluster = kdat$cluster
mdat = melt(ds, id.vars=c("cluster"))

imdb

ggplot(mdat, aes(fill=factor(cluster), x=value)) + 
  geom_histogram() + scale_x_log10()  + 
  facet_wrap(~variable, scales="free")

plot of chunk unnamed-chunk-48

imdb

ggplot(mdat, aes(factor(cluster), value)) + 
  geom_boxplot(outlier.shape=NA) + scale_y_log10() + 
  facet_wrap(~variable, scales="free_y")

plot of chunk unnamed-chunk-49

imdb

library(FNN)
closest = function(k){
  ds = dat_scaled[kdat$cluster ==k,]
  idx = get.knnx(ds, query = t(kdat$center[k,]))$nn.index[1]
  idx
  str(dat[kdat$cluster==k,][idx,])
}

imdb

closest(1)

'data.frame':   1 obs. of  29 variables:
 $ color                    : chr "Color"
 $ director_name            : chr "Andrzej Bartkowiak"
 $ num_critic_for_reviews   : int 109
 $ duration                 : int 101
 $ director_facebook_likes  : int 43
 $ actor_3_facebook_likes   : int 432
 $ actor_2_name             : chr "Tom Arnold"
 $ actor_1_facebook_likes   : int 5000
 $ gross                    : int 34604054
 $ genres                   : chr "Action|Crime|Drama|Thriller"
 $ actor_1_name             : chr "Jet Li"
 $ movie_title              : chr "Cradle 2 the Grave "
 $ num_voted_users          : int 34942
 $ cast_total_facebook_likes: int 6867
 $ actor_3_name             : chr "DMX"
 $ facenumber_in_poster     : int 2
 $ plot_keywords            : chr "camera shot from inside human body|diamond|evil man|heist|terrorism"
 $ movie_imdb_link          : chr "http://www.imdb.com/title/tt0306685/?ref_=fn_tt_tt_1"
 $ num_user_for_reviews     : int 185
 $ language                 : chr "English"
 $ country                  : chr "USA"
 $ content_rating           : chr "R"
 $ budget                   : num 3e+07
 $ title_year               : int 2003
 $ actor_2_facebook_likes   : int 618
 $ imdb_score               : num 5.8
 $ aspect_ratio             : num 2.35
 $ movie_facebook_likes     : int 1000
 $ cluster                  : int 1

imdb

closest(2)

'data.frame':   1 obs. of  29 variables:
 $ color                    : chr "Color"
 $ director_name            : chr "Gabriele Muccino"
 $ num_critic_for_reviews   : int 202
 $ duration                 : int 123
 $ director_facebook_likes  : int 125
 $ actor_3_facebook_likes   : int 835
 $ actor_2_name             : chr "Rosario Dawson"
 $ actor_1_facebook_likes   : int 10000
 $ gross                    : int 69951824
 $ genres                   : chr "Drama|Romance"
 $ actor_1_name             : chr "Will Smith"
 $ movie_title              : chr "Seven Pounds "
 $ num_voted_users          : int 232710
 $ cast_total_facebook_likes: int 14727
 $ actor_3_name             : chr "Madison Pettis"
 $ facenumber_in_poster     : int 1
 $ plot_keywords            : chr "boyfriend girlfriend relationship|heart|main character dies|organ donor|redemption"
 $ movie_imdb_link          : chr "http://www.imdb.com/title/tt0814314/?ref_=fn_tt_tt_1"
 $ num_user_for_reviews     : int 599
 $ language                 : chr "English"
 $ country                  : chr "USA"
 $ content_rating           : chr "PG-13"
 $ budget                   : num 5.5e+07
 $ title_year               : int 2008
 $ actor_2_facebook_likes   : int 3000
 $ imdb_score               : num 7.7
 $ aspect_ratio             : num 2.35
 $ movie_facebook_likes     : int 26000
 $ cluster                  : int 2

imdb

closest(3)

'data.frame':   1 obs. of  29 variables:
 $ color                    : chr "Color"
 $ director_name            : chr "Rupert Sanders"
 $ num_critic_for_reviews   : int 416
 $ duration                 : int 132
 $ director_facebook_likes  : int 274
 $ actor_3_facebook_likes   : int 11000
 $ actor_2_name             : chr "Kristen Stewart"
 $ actor_1_facebook_likes   : int 26000
 $ gross                    : int 155111815
 $ genres                   : chr "Action|Adventure|Drama|Fantasy"
 $ actor_1_name             : chr "Chris Hemsworth"
 $ movie_title              : chr "Snow White and the Huntsman "
 $ num_voted_users          : int 228554
 $ cast_total_facebook_likes: int 72881
 $ actor_3_name             : chr "Sam Claflin"
 $ facenumber_in_poster     : int 0
 $ plot_keywords            : chr "evil queen|fairy tale|magic|queen|snow white"
 $ movie_imdb_link          : chr "http://www.imdb.com/title/tt1735898/?ref_=fn_tt_tt_1"
 $ num_user_for_reviews     : int 710
 $ language                 : chr "English"
 $ country                  : chr "USA"
 $ content_rating           : chr "PG-13"
 $ budget                   : num 1.7e+08
 $ title_year               : int 2012
 $ actor_2_facebook_likes   : int 17000
 $ imdb_score               : num 6.1
 $ aspect_ratio             : num 2.35
 $ movie_facebook_likes     : int 53000
 $ cluster                  : int 3

imdb

Possible cluster labels?

Critically Acclaimed (higher imdb score and number of raters)
Popular with the Masses (higher fb likes, crowd pleaser)
Mediocre/mixed popularity